La symphonie des neurones ou les mathématiques du cerveau
Constitué d’environ 86 milliards de neurones connectés entre eux par des synapses 10000 fois plus nombreuses, le cerveau humain commande le corps à travers une symphonie électrochimique permanente. Mais comment les neurones individuels communiquent-ils entre eux pour apporter une réponse globale adéquate ? Pour répondre à cette question aujourd’hui, il semble nécessaire d’allier les recherches de neuroscientifiques, de physiciens et de mathématiciens.
Pour citer cet article :
Ambrosio Benjamin, Alaoui Aziz. La symphonie des neurones ou les mathématiques du cerveau. Philosophie, science et société. 2022. https://philosciences.com/synchronisation-neurones-mathematiques-cerveau.
Texte intégral :
Un article publié récemment dans la revue Nature montre comment le cerveau de la mouche effectue des calculs vectoriels pour gérer son orientation dans le plan bidimensionnel pendant son vol. Ces recherches ont mis en évidence une synchronisation en temps réel de l’activité neuronale de certaines zones du cerveau, ainsi que leur correspondance en termes de calcul vectoriel, pour permettre à la mouche de s’orienter dans le plan.
Des groupes de neurones se synchronisent
D’une manière générale, deux phénomènes apparaissent aujourd’hui comme incontournables lorsque l’on souhaite étudier l’activité de groupes de neurones dans le cerveau : la synchronisation et l’émergence de rythmes.
Pour des réseaux constitués d’éléments semblables, comme le cerveau, la synchronisation renvoie à l’idée d’une cohérence d’activité entre les différents éléments du système. On observe plusieurs types de synchronisation dans les systèmes physiques et la nature. Par exemple, il est possible d’observer des groupes de lucioles qui émettent des signaux lumineux de manière synchronisée ou bien des bancs de poissons ou essaims d’oiseaux qui synchronisent leurs mouvements.
On parle de « synchronisation complète » lorsque tous les éléments du système évoluent de manière identique au cours du temps. C’est la synchronisation la plus frappante. Ce type de synchronisation correspond par exemple à une assemblée de métronomes qui, disposés sur une planche de bois assise sur des canettes de soda, vont synchroniser leurs oscillations de manière identique.
Dans le cerveau, les synchronisations sont différentes et plus subtiles.
Et un rythme émerge
Les rythmes qui émergent peuvent être identifiés : ils correspondent à des fréquences, comme si les neurones prenaient le rôle des métronomes. Le cerveau abonde d’exemples d’émergence de synchronisations et de rythmes : par exemple, le système cortex visuel V1, une zone située à l’arrière du cerveau qui reçoit les signaux visuels, est très étudié.
Les expériences montrent que l’on observe un pic de fréquence gamma (c’est-à-dire supérieure à 30 hertz) lorsqu’on stimule le cortex visuel V1 grâce à des signaux visuels spécifiques, par exemple des images avec des lignes noires et blanches se déplaçant dans une direction donnée. Des modèles mathématiques constitués de réseaux d’équations différentielles ordinaires sont utilisés pour modéliser l’activité de V1.
Des travaux récents ont montré grâce à ce type de modèle comment la stimulation de V1 peut entraîner l’émergence de rythmes gamma via une synchronisation partielle de l’activité neuronale. Dans ce cas, le rythme émerge de l’augmentation du nombre de potentiels d’action (des impulsions) émis de manière concomitante dans des sous-groupes de la population neuronale.
Ici, il ne s’agit pas de synchronisation complète, car tous les neurones n’adoptent pas une dynamique identique. Des groupes de neurones vont au cours du temps avoir tendance à émettre simultanément des potentiels d’actions, ce qui va produire le rythme observé dans le réseau.
Les mathématiques du cerveau
Ce type de modèle mathématique constitué d’un réseau d’entités individuelles fait partie de la catégorie des systèmes complexes. Lorsqu’on étudie les systèmes complexes, on cherche typiquement à comprendre comment, pour une certaine structure de réseau, des entités individuelles et un niveau de stimulation donnés, la variation d’un paramètre va permettre l’émergence de synchronisations et de rythmes.
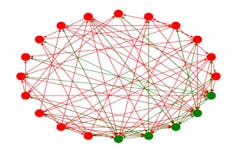
C’est l’objet d’un travail récent effectué dans le cadre d’une thèse, dans lequel nous avons considéré un réseau d’équations différentielles de type Hodgkin-Huxley (un modèle mathématique typique de neurone), dont la structure est inspirée par le cortex visuel V1. Dans ce réseau, chaque équation différentielle représente un neurone qui peut exciter ou inhiber l’activité électrique des neurones auxquels il est connecté.
En variant un paramètre (dans notre cas, un nombre quantifiant l’amplitude d’excitation induite par les neurones excitateurs vers les neurones excitateurs), on peut illustrer comment le système évolue d’un état non synchronisé vers un état de synchronisation partielle puis une synchronisation très prononcée. La fréquence du réseau est une fréquence de type gamma.
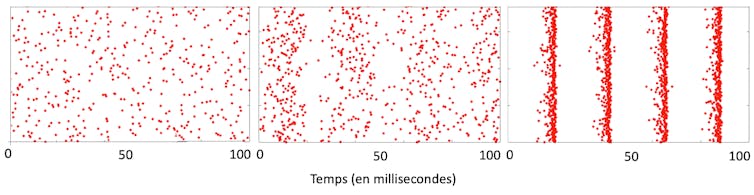
De telles approches, qui utilisent les mathématiques pour décrire l’émergence de fréquence dans les tissus neuronaux devraient se développer de plus en plus dans le futur. Une des applications très concrètes de ces modèles est de calibrer la valeur des paramètres pour permettre une implémentation optimale de solutions thérapeutiques. Par exemple, les techniques de stimulation électrique ou électromagnétique sont très étudiées dans des contextes tels que la thérapeutique des aphasies ou de la maladie de Parkinson.
Il faut préciser ici que les modèles mathématiques doivent s’adapter aux différentes échelles spatiales selon le type de mesures effectuées, de l’échelle de la surface crânienne à quelques millimètres dans d’autres études.
Il n’en demeure pas moins que les modèles mathématiques capables de reproduire des fréquences typiques mesurées dans le cerveau à différentes échelles sont amenés à jouer un rôle crucial dans la compréhension de l’émergence des rythmes cérébraux.![]()
Les auteurs :
Benjamin Ambrosio, Maître de conférences en mathématiques, Université Le Havre Normandie et Aziz Alaoui, Professeur de mathématiques appliquées, Université Le Havre Normandie
Cet article est republié à partir de The Conversation sous licence Creative Commons.